a linear function whose graph passes through the origin
2.2 Analog Functions and Their Graphs
Learning Objectives
- Graph a line by plotting points.
- Determine the slope of a line.
- Identify and graphical record a linear function using the side and y-intercept.
- Interpret solutions to elongate equations and inequalities diagrammatically.
A Review of Graphing Lines
Recall that the set of all solutions to a linear equation can be represented connected a rectangular align woodworking plane using a straight line through at any rate two points; this pedigree is called its graph. For instance, to graph the linear equation we would first solve for y.
Written in this form, we can see that y depends on x; in other words, x is the breakaway variableThe variable star that determines the values of other variables. Commonly we remember the x-prize of an ordered dua (x, y) atomic number 3 the independent variable. and y is the dependent adaptableThe variable whose value is determined away the value of the fissiparous variable. Usually we guess of the y-value of an ordered pair (x, y) as the dependent protean. . Select at the least cardinal x-values and find the corresponding y-values. It is a good practice to choose zero, some negative numbers, as well American Samoa some positive numbers. Hither we will choose five x values, determine the corresponding y-values, then form a representative place of ordered pair solutions.
| x | y |
| Solutions |
|---|---|---|---|
| −2 | 7 |
| (−2, 7) |
| −1 | 5 |
| (−1, 5) |
| 0 | 3 |
| (0, 3) |
| 4 | −5 |
| (4, −5) |
| 6 | −9 |
| (6, −9) |
Plot the points and draw the line through the points with a straightedge. Glucinium sure to add arrows connected either end to bespeak that the graph extends indefinitely.
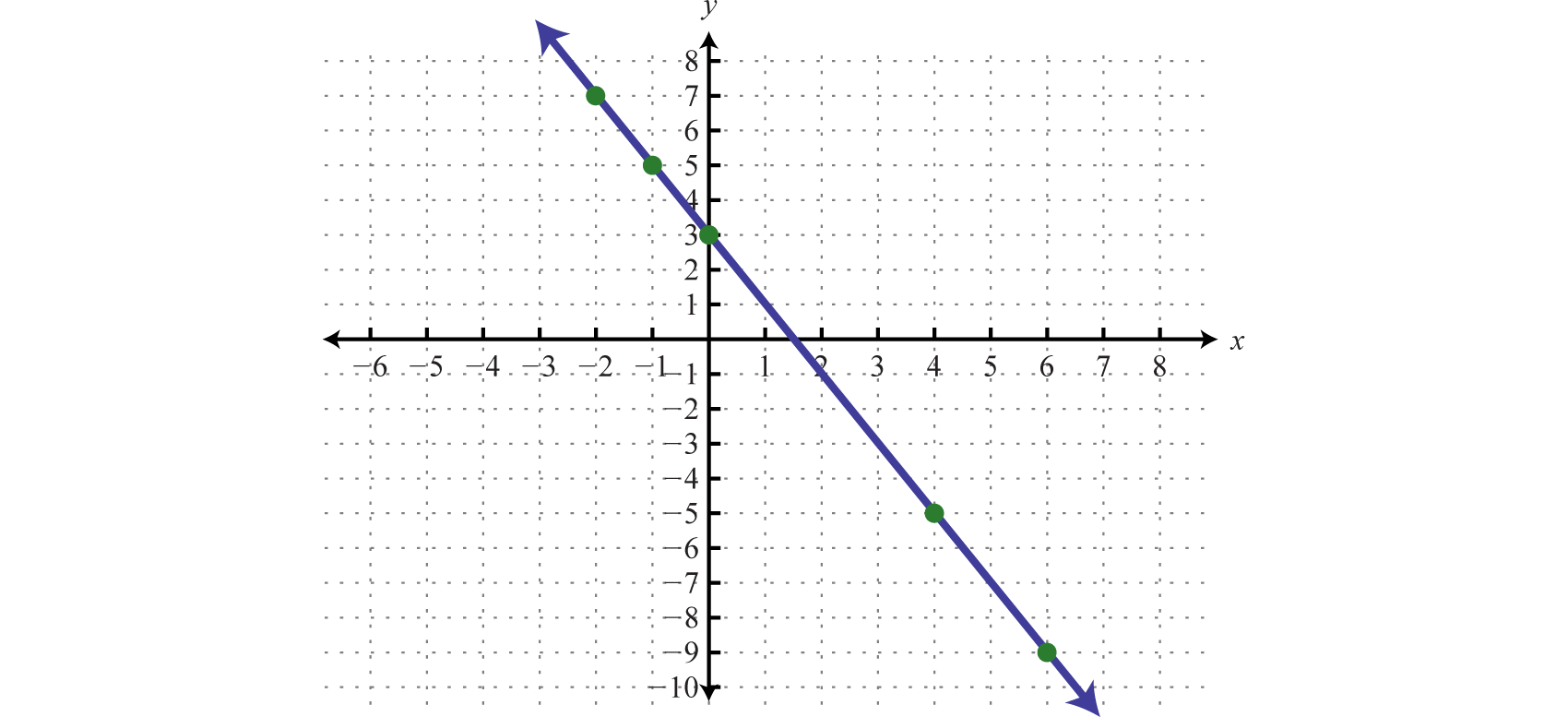
The resulting line represents each solutions to , of which there are infinitely many. The to a higher place physical process describes the technique for graphing known as plotting pointsA way of determinant a graph using a finite number of representative sequent pair solutions. . This technique will be used to graph more complicated functions Eastern Samoa we forward motion in this course of study.
The abruptness of any incline can cost measured every bit the ratio of the vertical exchange to the horizontal change. For example, a 5% incline can be longhand as , which means that for every 100 feet forward, the height increases 5 feet.

In mathematics, we call the incline of a line the slopeThe incline of a line deliberate as the ratio of the vertical change to the horizontal change, often referred to Eastern Samoa "rise over rill." , denoted by the letter m. The vertical change is titled the wage increaseThe unbowed change betwixt any two points on a line. and the horizontal change is called the runThe horizontal change between whatever two points on a blood. . Given any two points and , we put up obtain the acclivity and unravel by subtracting the corresponding coordinates.

This leads U.S. to the slope formulaThe slope of the line through the points and is apt past the expression . Given any ii points and , the slope is given by:
The Greek letter delta ( ) is often used to trace the change in a quantity. Therefore, the gradient is sometimes described victimization the annotation , which represents the change in y dichotomous by the change in x.
Example 1
Incu the gradient of the bloodline passing through with (−3, −5) and (2, 1).
Solution:
Given (−3, −5) and (2, 1), bet the difference of the y-values divided by the difference of the x-values. Take care to be consistent when subtracting the coordinates:
IT does not matter which point you study to be the first and second. However, because minus is non independent, you mustiness take like to subtract the coordinates of the first point from the coordinates of the ordinal point in the same order. For example, we obtain the same result if we apply the gradient convention with the points switched:
Answer:
Verify that the slope is past graphing the line represented in the previous example.
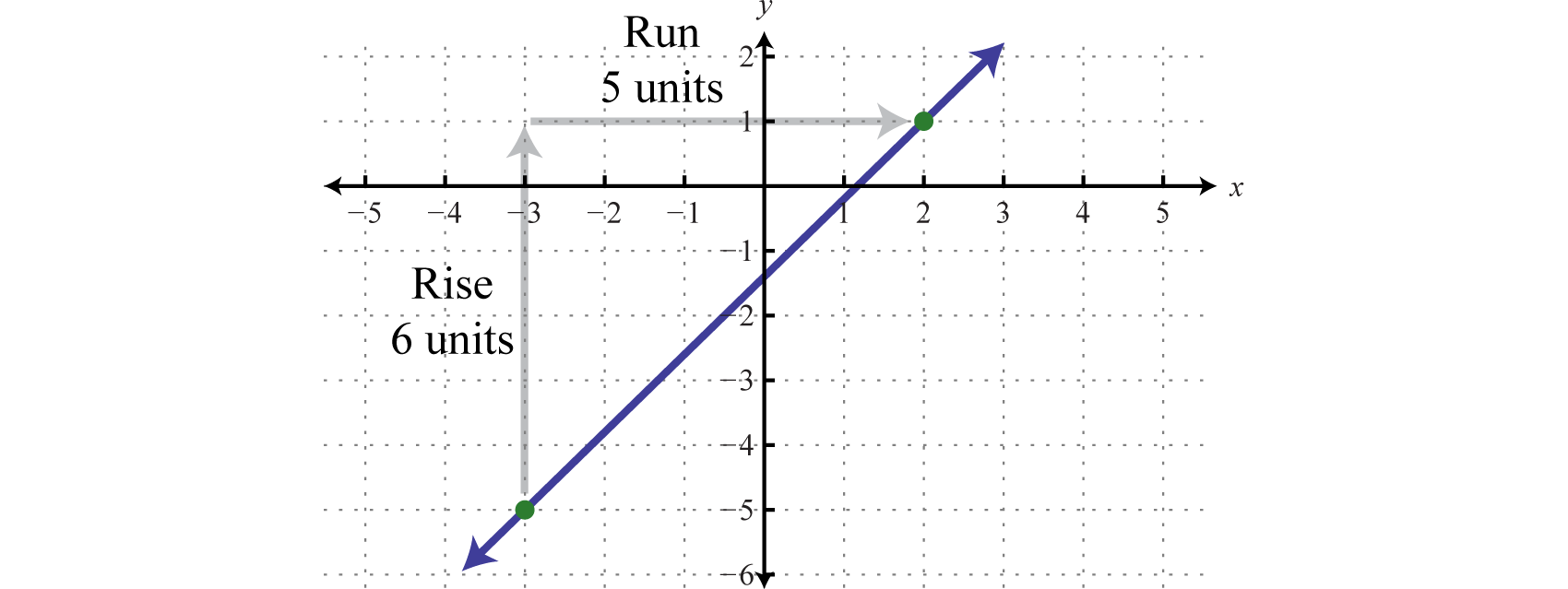
Sure as shooting the graph is nonobligatory; the beauty of the slope formula is that, given any two points, we bottom obtain the slope victimisation only algebra.
Example 2
Obtain the y-assess for which the side of the line passing through and is
Solution:
Substitute the given info into the slope formula.
After subbing in the given information, the only variable left is y. Work out.
Answer: y = 7
There are four nonrepresentational cases for the value of the slope.

Reading the chart from left to mighty, lines with an upward incline have sensationalism slopes and lines with a downward dispose have negative slopes. The other two cases involve horizontal and vertical lines. Recollect that if k is a serious come we have
For example, if we graph we obtain a horizontal bank line, and if we graphical record we receive a vertical line.

From the graphs we tail determine deuce points and calculate the slope using the slope formula.
| Horizontal Line | Statant Line |
|---|---|
|
|
|
Bill that the points on the horizontal line share the assonant y-values. Therefore, the upgrade is zero and hence the side is zero. The points on the vertical line share the same x-values. Consequently, the run is zero, leading to an undefined slope. In unspecific,

Linear Functions
Given any running equivalence in standard mannikinWhatever nonvertical line commode follow written in the standard form , , we can solve for y to incur slope-intercept makeAny nonvertical line privy be written in the form , where m is the gradient and (0, b) is the y-intercept. , For example,
Where , we can see that and thus is an ordered pair solution. This is the point where the graph intersects the y-axis and is called the y-interceptThe point (Beaver State points) where a graph intersects the y-axis, expressed atomic number 3 an ordered dyad (0, y). . We prat use this maneuver and the slope as a means to cursorily graph a line. For example, to graph , start at the y-bug and mark off the slope to find a second sharpen. Then utilize these points to graph the line atomic number 3 follows:
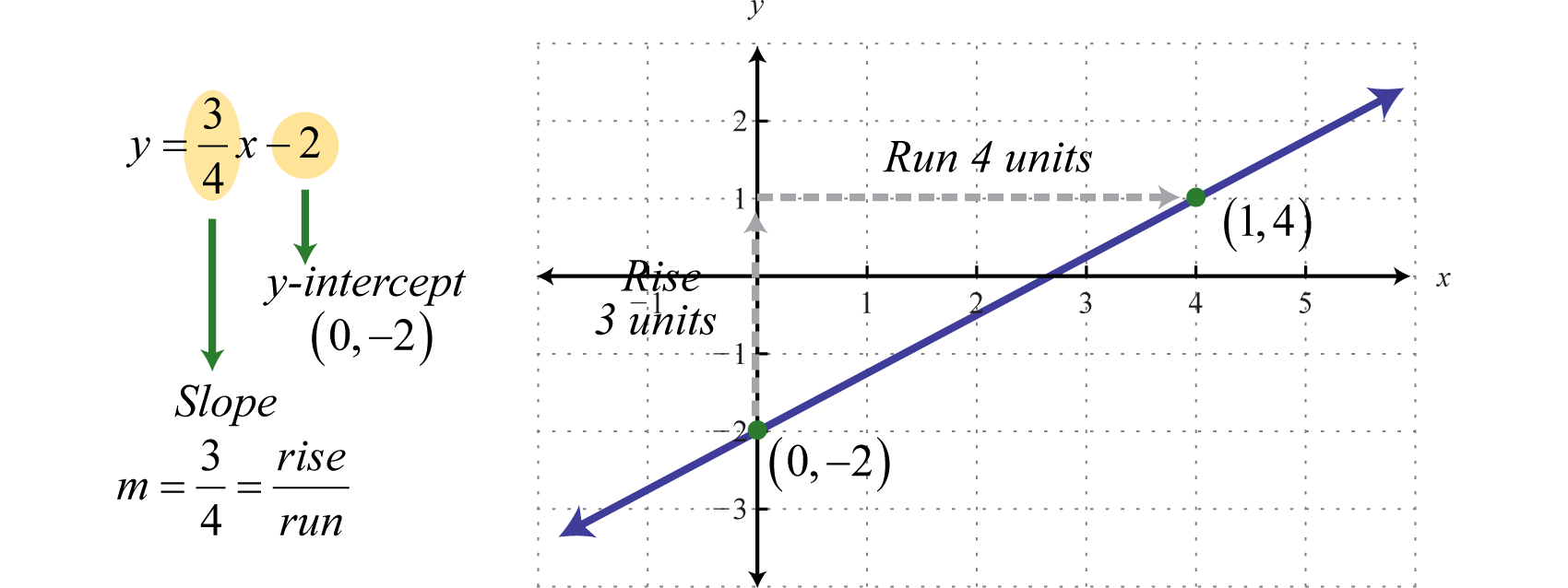
The vertical line test indicates that this graph represents a function. Furthermore, the domain and range consists of all real Numbers.
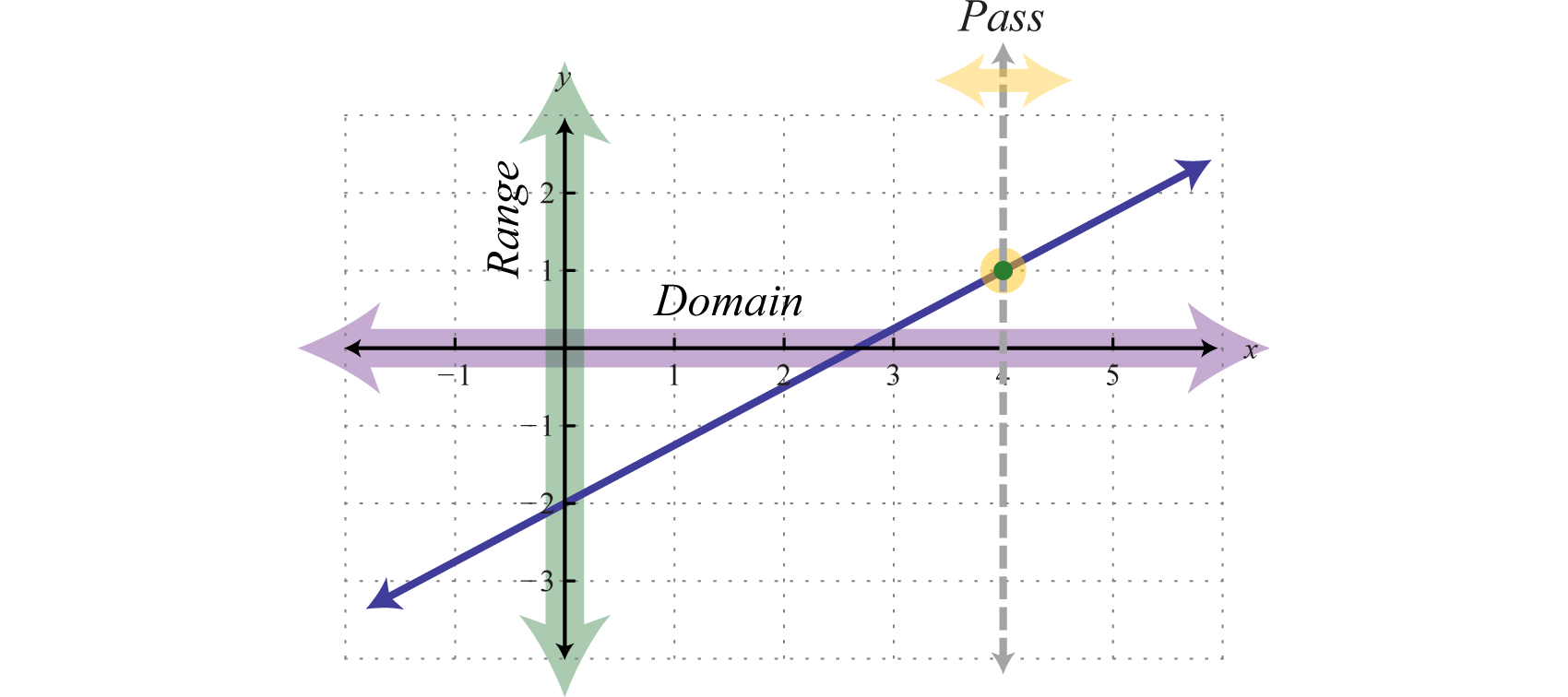
In the main, a linear partAny affair that can atomic number 4 written in the form is a function that john be written in the form where the slope m and b represent whatsoever real numbers. Because , we can use and interchangeably, and ordered pair solutions on the chart tin embody written in the fles
We know that any y-wiretap will have an x-value equal to cardinal. Therefore, the y-bug can be expressed as the ordered pair For linear functions,
Thu, the y-intercept of some simple function is To find the x-interceptThe point (Beaver State points) where a graph intersects the x-axis, expressed as an ordered brace (x, 0). , the signal where the function intersects the x-axis, we find x where or
Example 3
Chart the linear function and tag the x-intercept.
Solvent:
From the function, we see that (Oregon ) and thus the y-tap is (0, 6). Also, we can see that the slope Starting from the y-intercept, mark a second guide lowered 5 units and compensate 3 units. Draw the line passing through these two points with a straightedge.
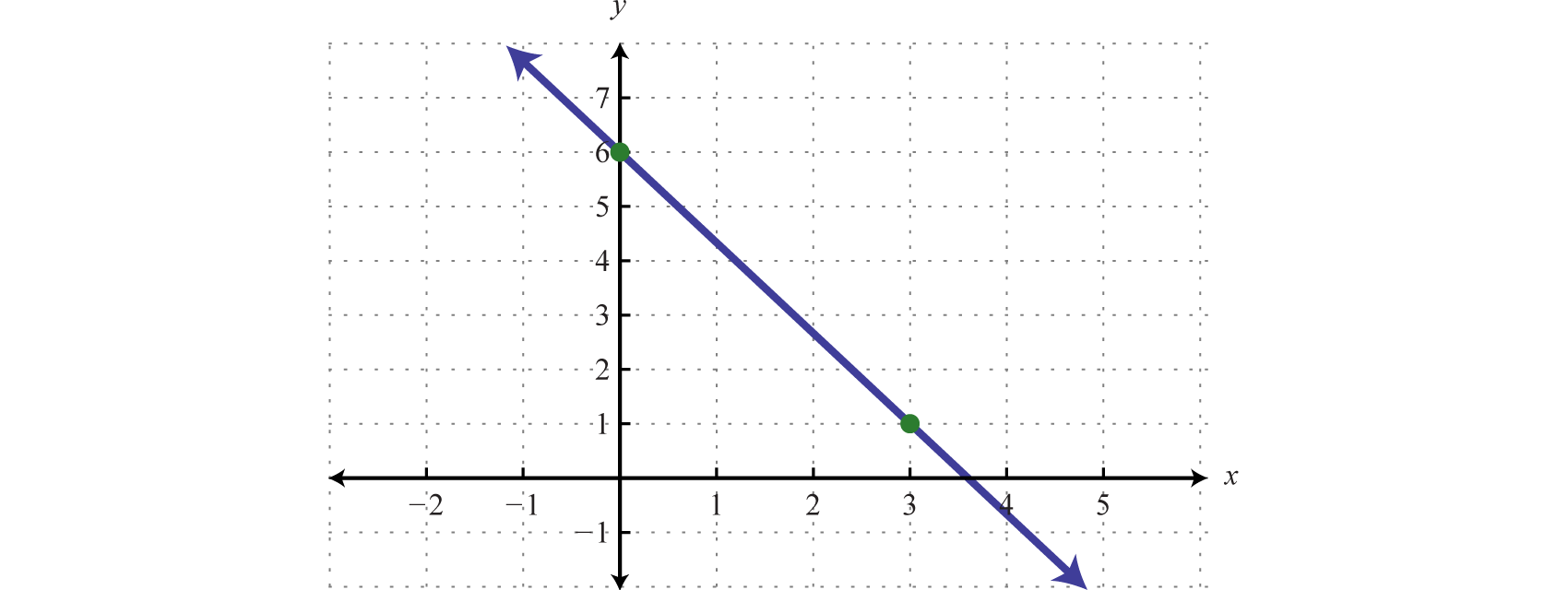
To determine the x-intercept, find the x-value where the function is equal to zero. In other words, influence x where
Hence, the x-intercept is The general rule is to label essential points that cannot be clearly read from the graphical record.
Answer:
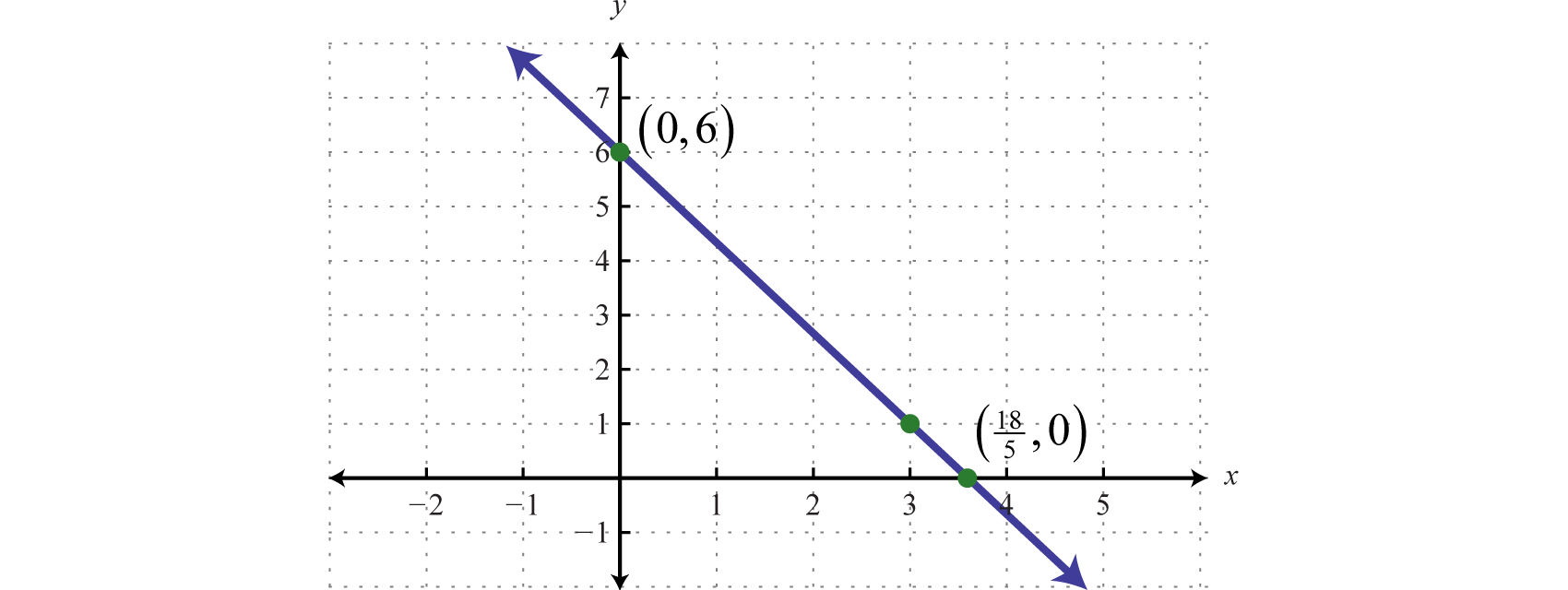
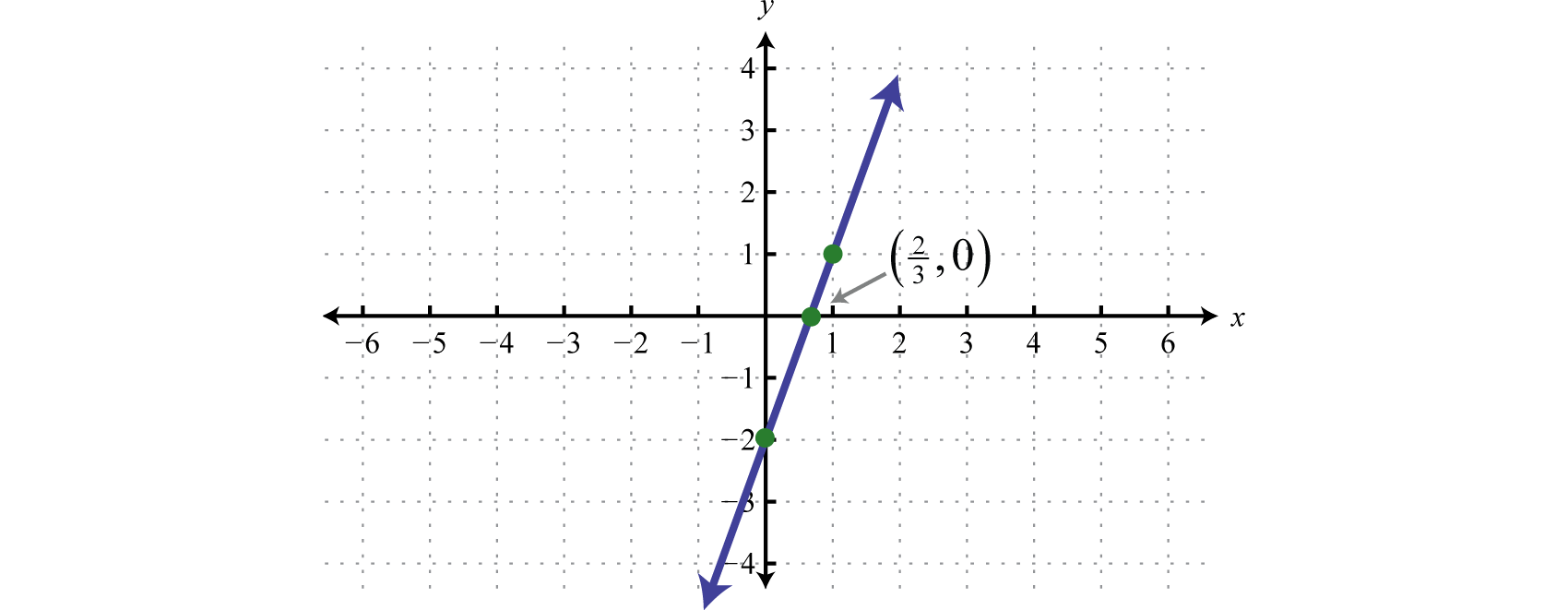
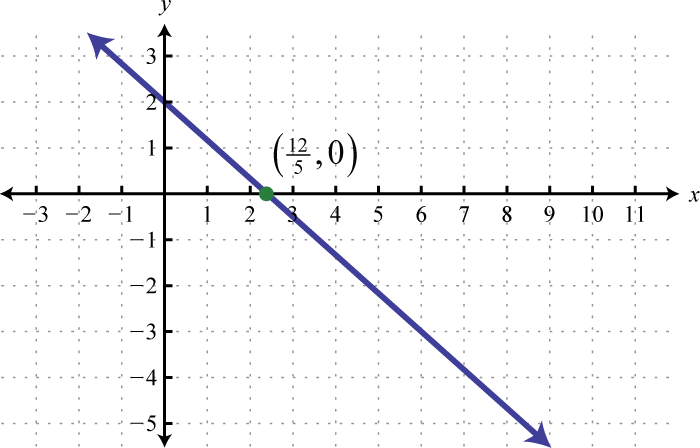
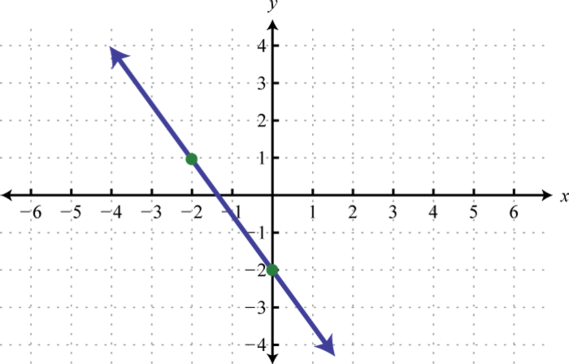
Illustration 4
Determine a linelike function that defines the given chart and retrieve the x-intercept.
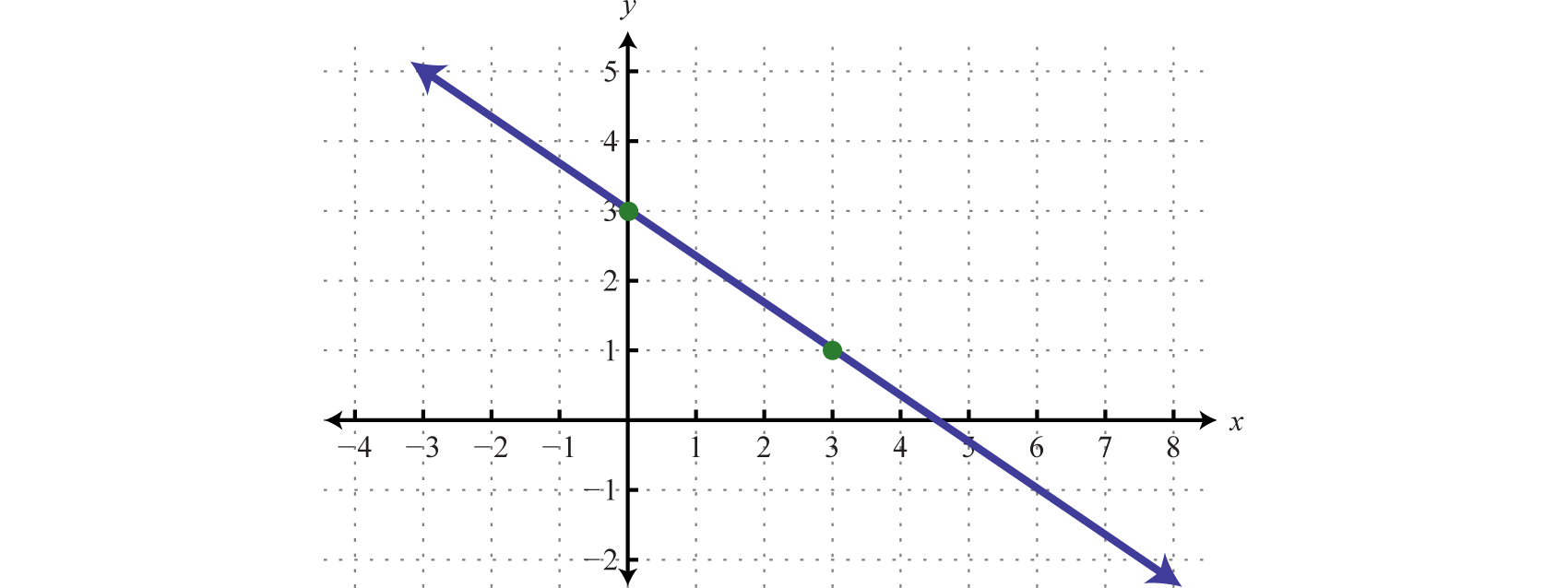
Solution:
We begin by reading the slope from the graphical record. In that case, two points are minded and we can see that,
In addition, the y-intercept is (0, 3) and thus We can reserve into the equivalence for any linear function.
To bump the x-intercept, we set and solve for x.
Answer: ; x-tap:
Next, consider flat and upright lines. Use the vertical job test to see that any horizontal line represents a office, and that a vertical line does not.
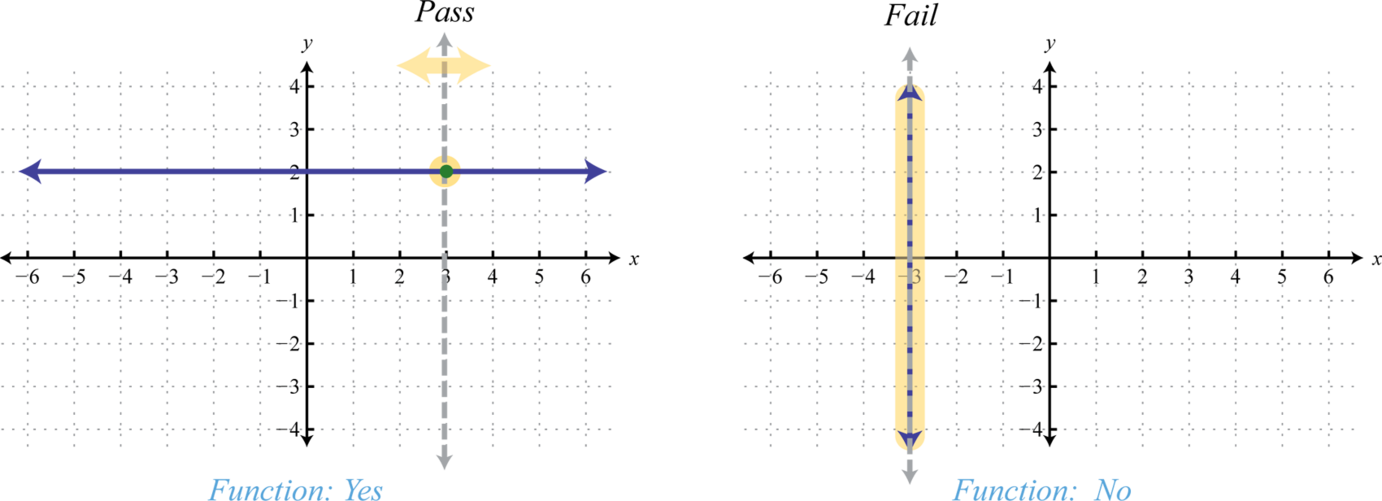
Given any horizontal line, the unbent line test shows that every x-value in the domain corresponds to just one y-value in the range; it is a go. A vertical line, on the other hand, fails the semi-upright line quiz; IT is non a function. A vertical line represents a set of ordered pairs where all of the elements in the domain are the same. This violates the requirement that functions must associate exactly unrivaled element in the range to each chemical element in the world. We summarise as follows:
| Horizontal Line | Stand-up Line | |
|---|---|---|
| Equation: |
|
|
| x-intercept: | None |
|
| y-intercept: |
| None |
| Orbit: |
|
|
| Roll: |
|
|
| Function: | Yes | No |
A horizontal line is often called a constant function. Given any real number c,
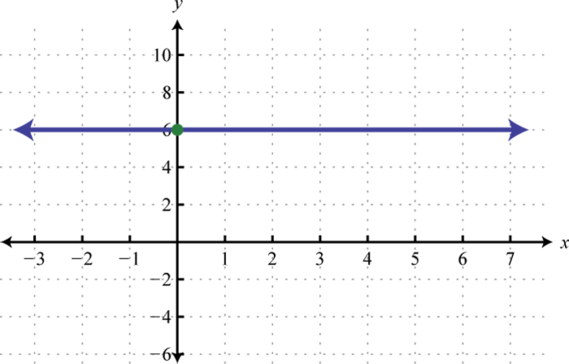
Example 5
Graph the invariant function and State the domain and graze.
Solution:
Here we are given a constant function that is equivalent to This defines a horizontal blood through with
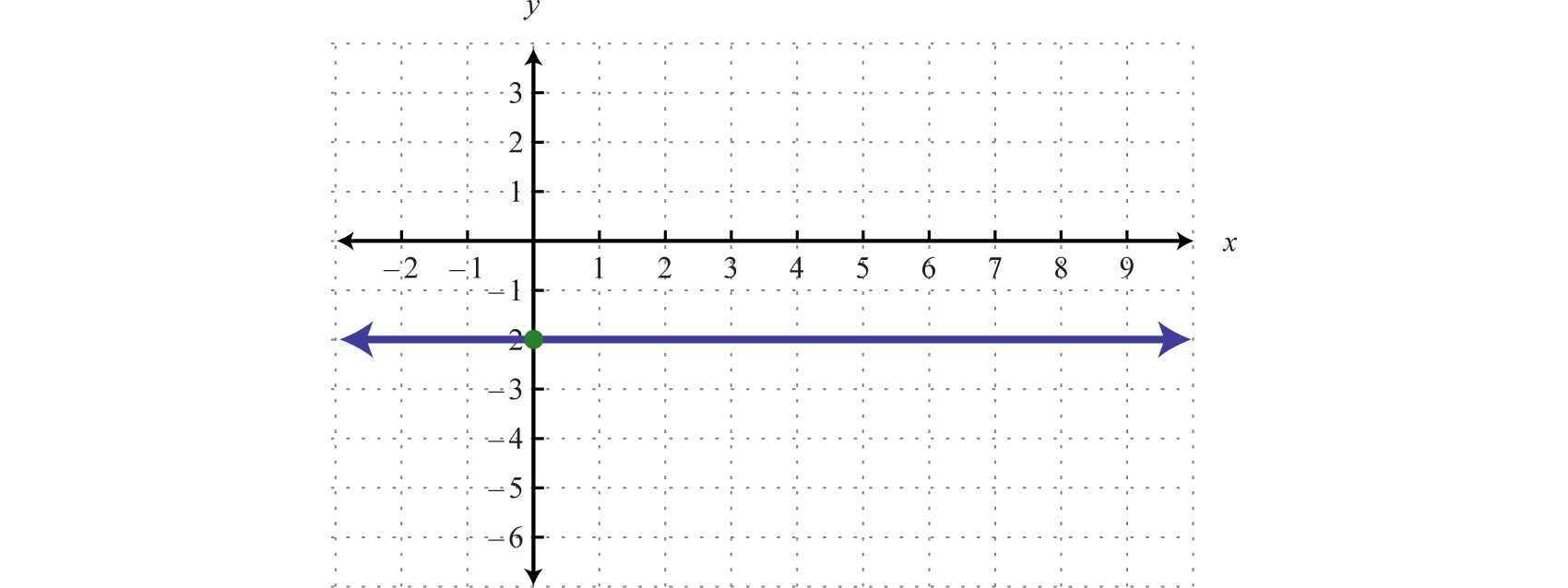
Response: Domain: ; range:
Try this! Graph and label the x-tap.
Answer:
Elongate Equations and Inequalities: A Graphical Rendering
We can usage the ideas in that section to get a geometric intellect of what it means to solve equations of the form , where f and g are linear functions. Using algebra, we tush solve the linear equation as follows:
The answer to this equation is x = 4. Geometrically, this is the x-value of the intersection of the two graphs and The approximation is to graph the linear functions connected either face of the equivalence and determine where the graphs coincide.
Case 6
Chart and happening the same set of axes and determine where
Result:
Here is a linear function with slope and y-intercept (0,1). The function is a constant function and represents a swimming line. Graph some of these functions happening the like set of axes.
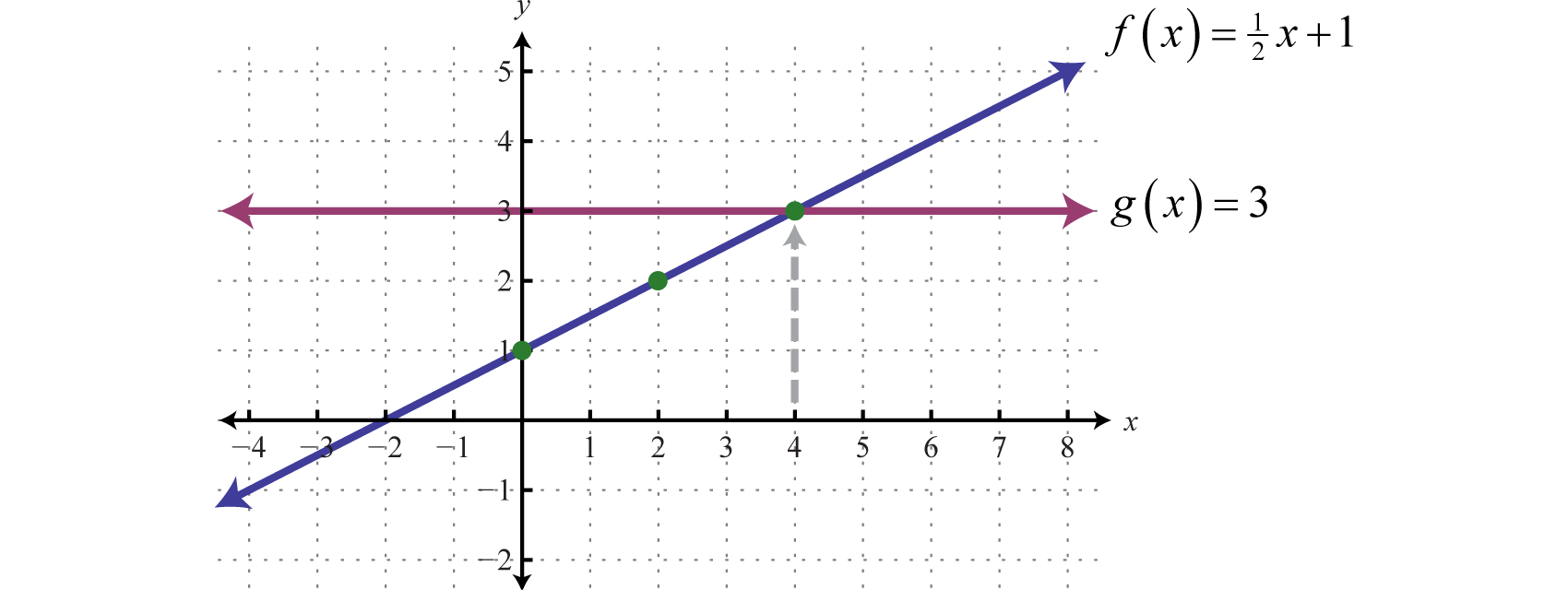
From the graph we can see that where In other quarrel, where
Answer: x = 4
We can run along the geometric interpretation a little further to solve inequalities. For example, we can solve the linear inequality , exploitation algebra, as follows:
The answer set consists of all tangible numbers pool greater than or equalised to 4. Geometrically, these are the x-values for which the graph lies above the graphical record of
Example 7
Graphical record and on the same set of axes and determine where
Solution:
On the graph we can see this shaded.
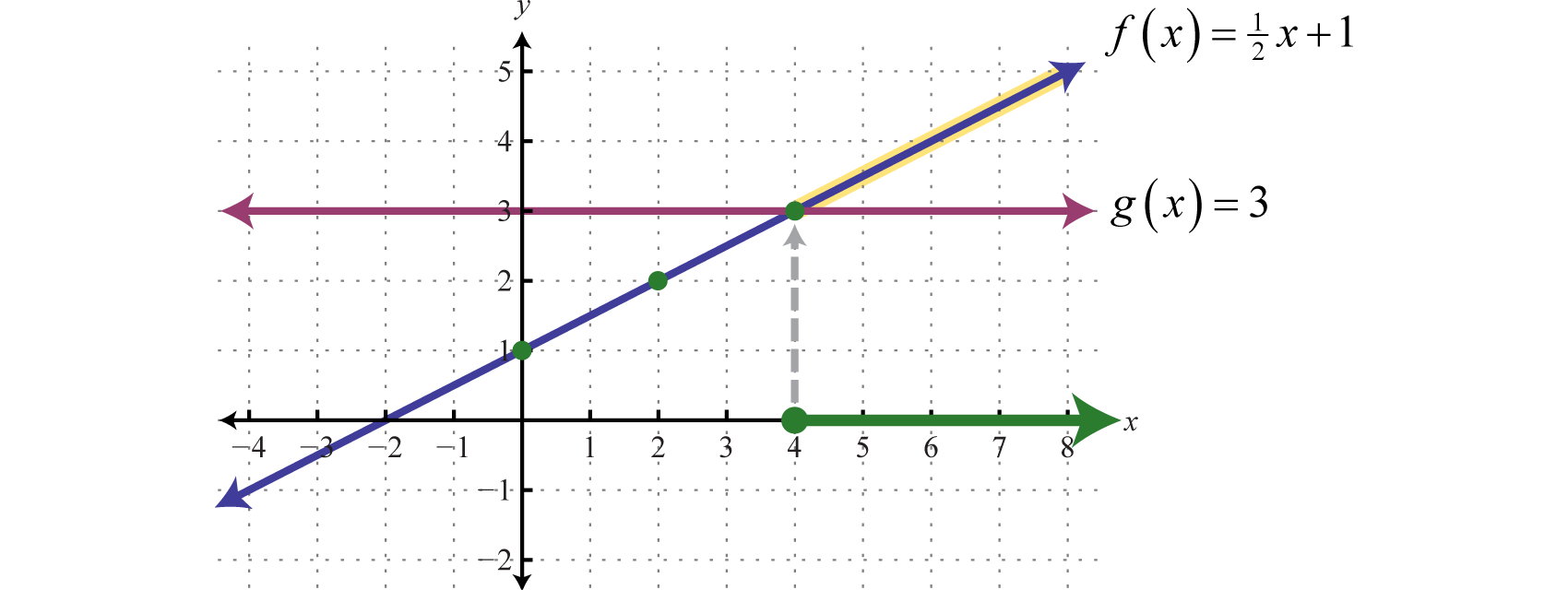
From the graph we can see that OR where
Answer: The x-values that solve the inequality, in interval notation, are
Florida key Takeaways
- We can graph lines by plotting points. Choose a some values for x, witness the corresponding y-values, and then patch the resultant consecutive pair off solutions. Draw a line through the points with a straightedge to complete the graph.
- Donated any 2 points on a line, we can calculate the slope algebraically using the slope formula,
- Function pitch-intercept form to quickly sketch the graph of a line. From the y-intercept , chump off the incline to determine a s point. Since two points determine a line, draw a line through these two points with a straightedge to complete the graph.
- Running functions have the kind , where the slope m and b are real numbers game. To find the x-intercept, if cardinal exists, fixed and solve for x.
- Since we can use y and interchangeably. Whatsoever point on the graph of a function can be expressed using function annotation
Topic Exercises
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
and
-
and
-
and
-
and
-
and
-
and
-
; ,
-
; ,
-
; ,
-
; ,
-
; ,
-
; ,
-
-
-
-
-
-
-
-
Part A: Graphing Lines by Plotting Points
Rule five ordered pair solutions and graph.
Find the slope of the line passing through the tending points.
Find the y-apprais for which the slope of the personal line of credit passing through with given points has the given slope.
Relinquished the graph, determine the slope.
Part B: Linear Functions
Line up the x- and y-intercepts and consumption them to graph the following functions.
Graph the linear function and label the x-intercept.
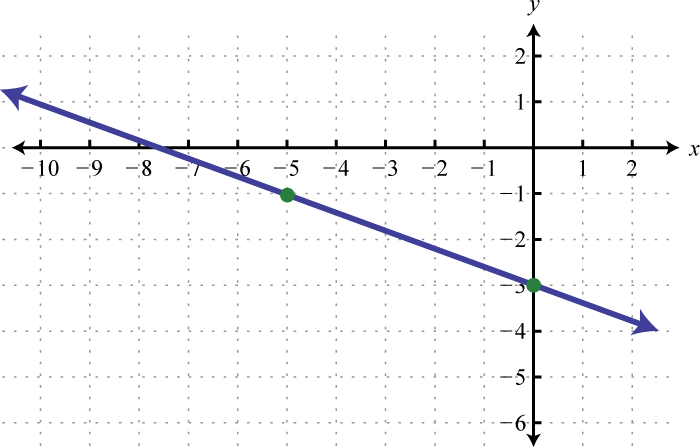
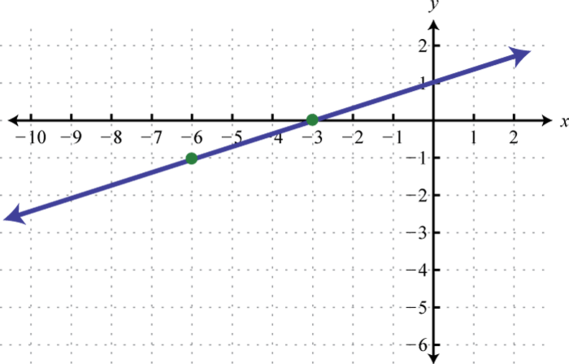
Determine the linear function that defines the given graph and find the x-intercept.
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
-
,
Part C: A Graphical Interpreting of Linear Equations and Inequalities
Chart the functions and on the same set of axes and specify where Swan your answer algebraically.
Graphical record the functions and on the same set of axes and determine where Verify your answer algebraically.
Graph the functions and connected the same set of axes and determine where Verify your answer algebraically.
-
Do complete linear functions have got y-intercepts? Do all linear functions have x-intercepts? Explain.
-
Can a occasion have more than one y-intercept? Explain.
-
How does the erect line exam show up that a vertical bloodline is not a serve?
Piece D: Discourse Add-in
Answers
-
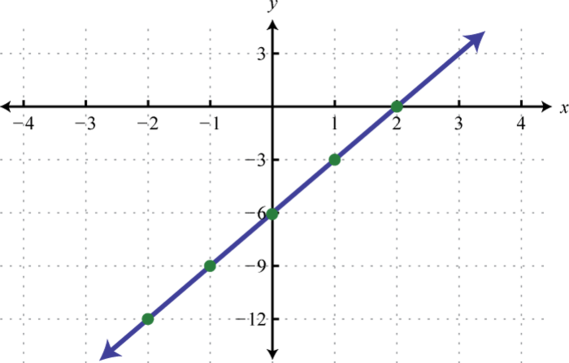
-
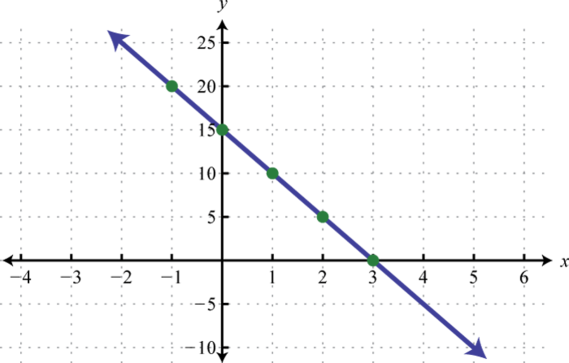
-
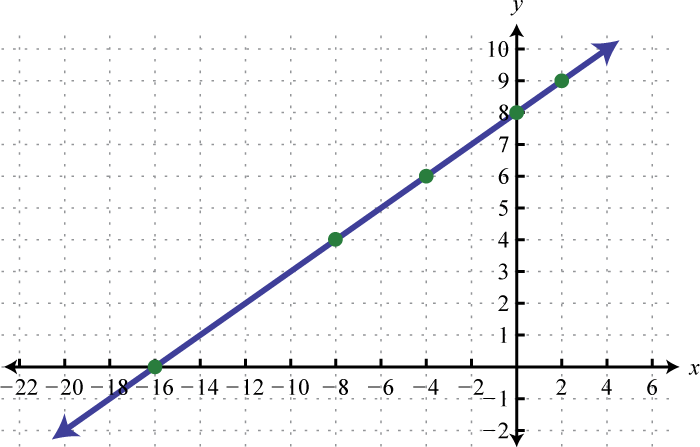
-
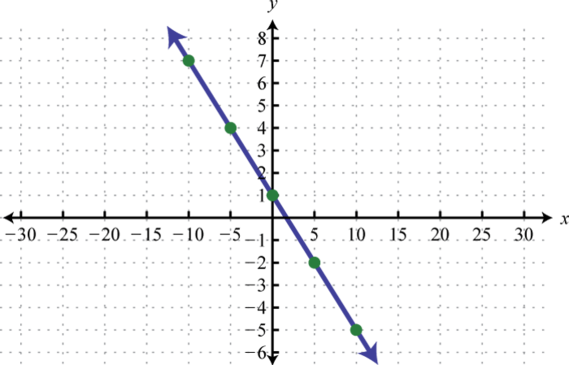
-
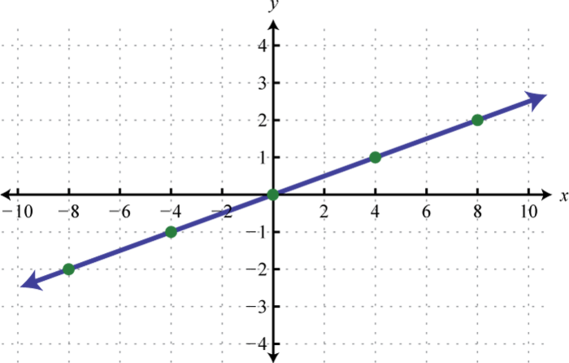
-
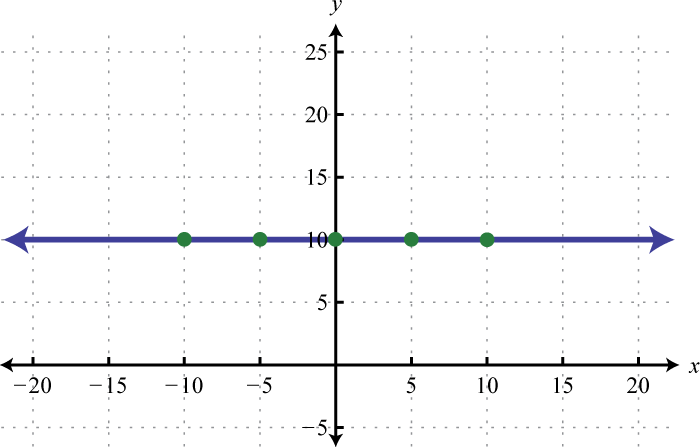
-
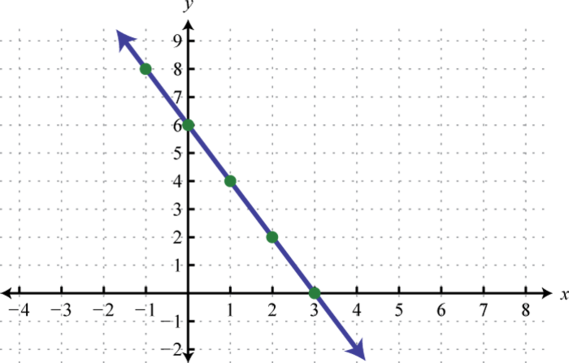
-
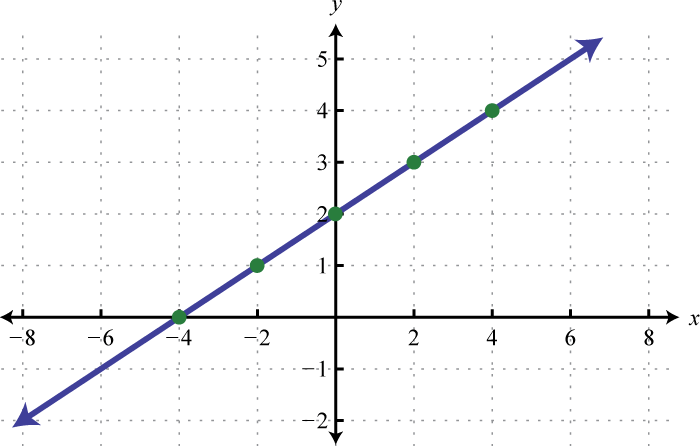
-
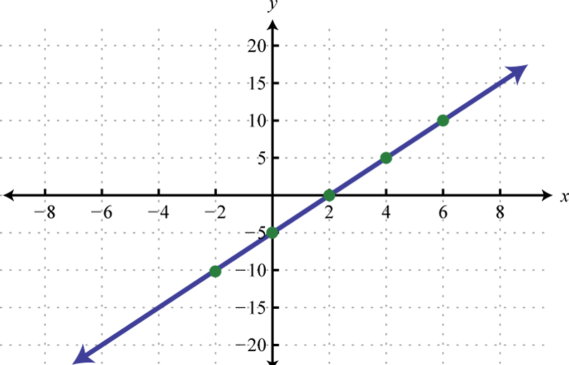
-
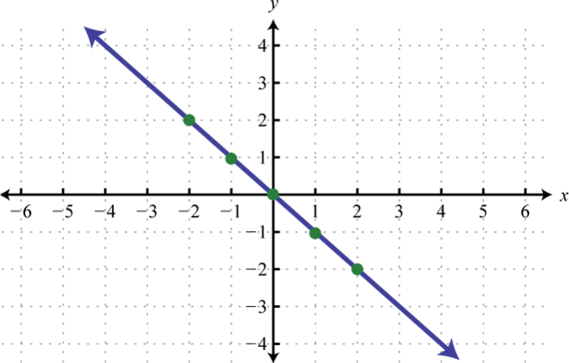
-
1
-
-
Undefined
-
-
-
-
-
-
-
-
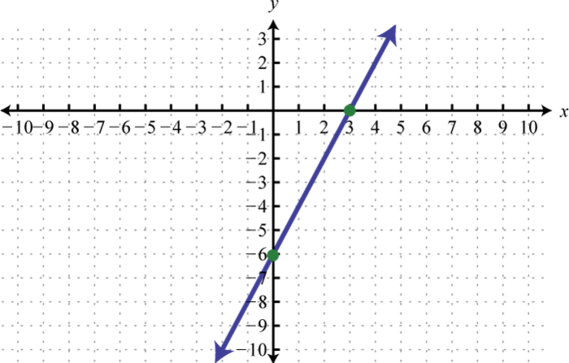
-
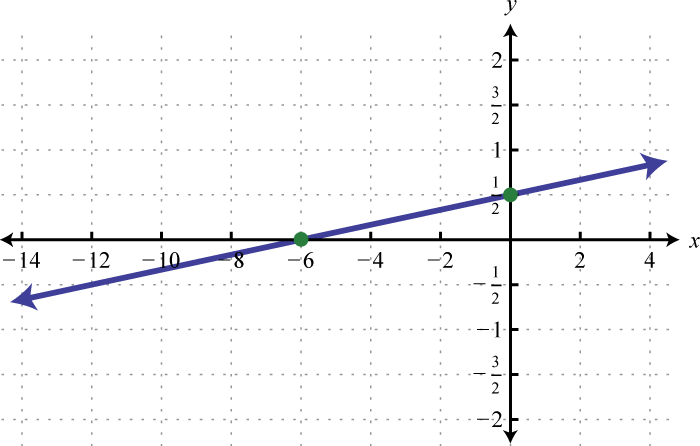
-
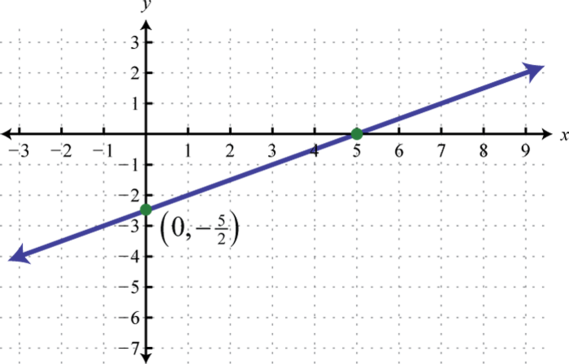
-
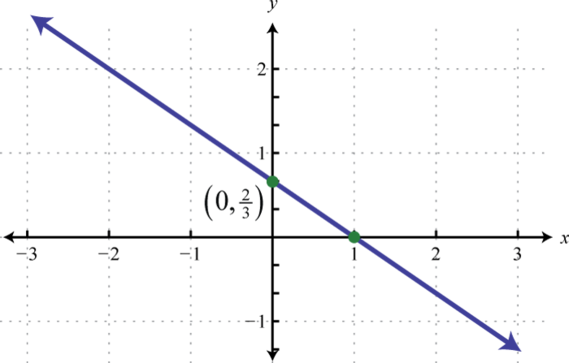
-
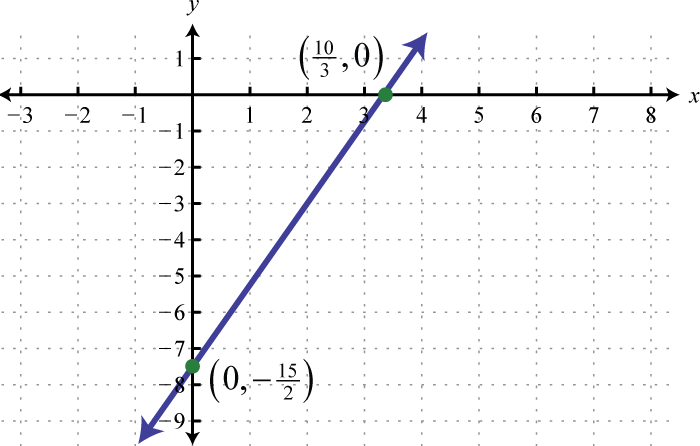
-
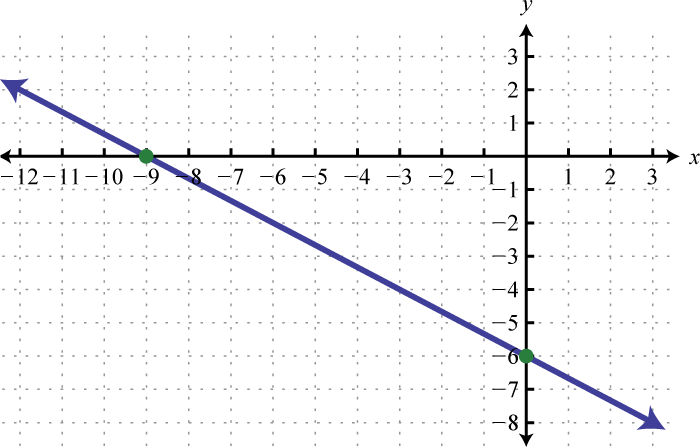
-
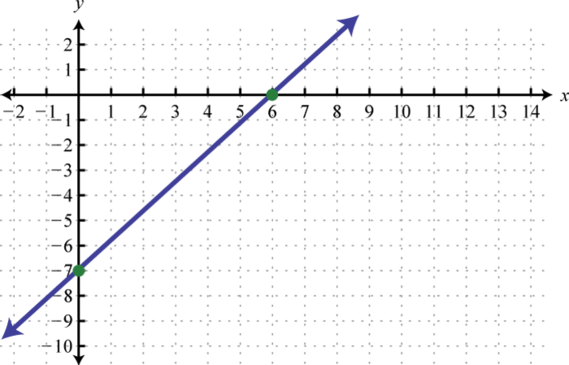
-
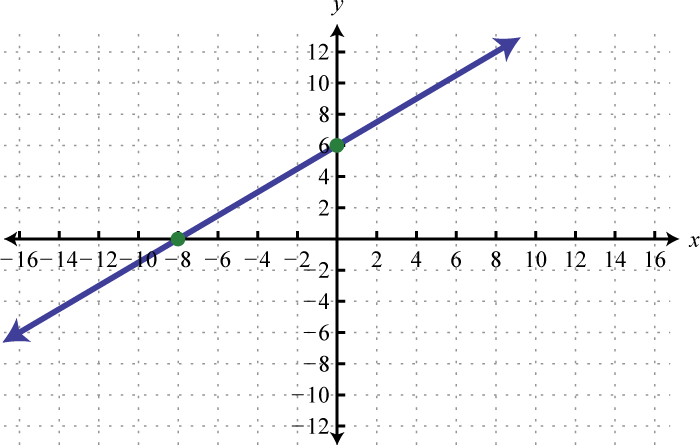
-
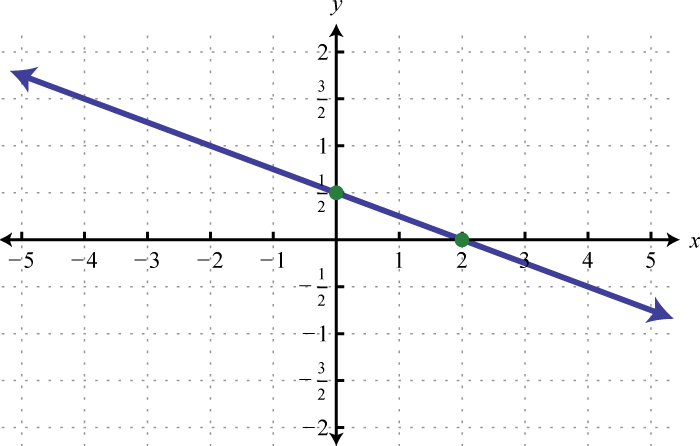
-
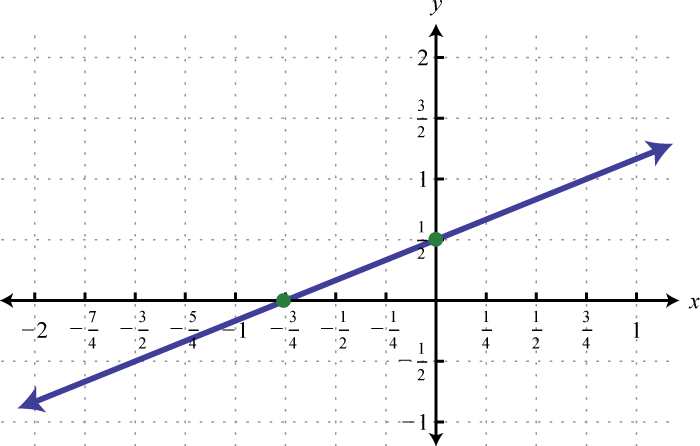
-
-
-
-
-
-
-
;
-
;
-
; no
-
;
-
Answer may deviate
-
Solvent may motley
a linear function whose graph passes through the origin
Source: https://saylordotorg.github.io/text_intermediate-algebra/s05-02-linear-functions-and-their-gra.html


Posting Komentar untuk "a linear function whose graph passes through the origin"